This person has found an actual solution:
https://mlzeng.com/an-interesting-equation.html
x = 36875131794129999827197811565225474825492979968971970996283137471637224634055579
y = 154476802108746166441951315019919837485664325669565431700026634898253202035277999
z = 4373612677928697257861252602371390152816537558161613618621437993378423467772036
This is apparently the smallest solution.
The derivation of the solution itself requires an understanding of Diophantine equations and elliptical curves, which I will not pretend to understand well enough to summarize.
From the same article, this is a solution when negative integers are allowed:
{{x -> 11, y -> 9, z -> -5}}
1, 1 and 7. The sum is 3.75 – take it or leave it.
Good enough for engineers.
Electronic engineers will know that 1, 1, 8 is closer but will go for 1, 1, 6.8 because they are in the E6 series and that will save 0.1 cents per device.
1, 1, 6.8
“6.8 isn’t an integer”
“It rounds to an integer”
“The tolerance is 5% so an integer is in range”
🍎=376556443707
🍌=50000000000
🍍=50000000000
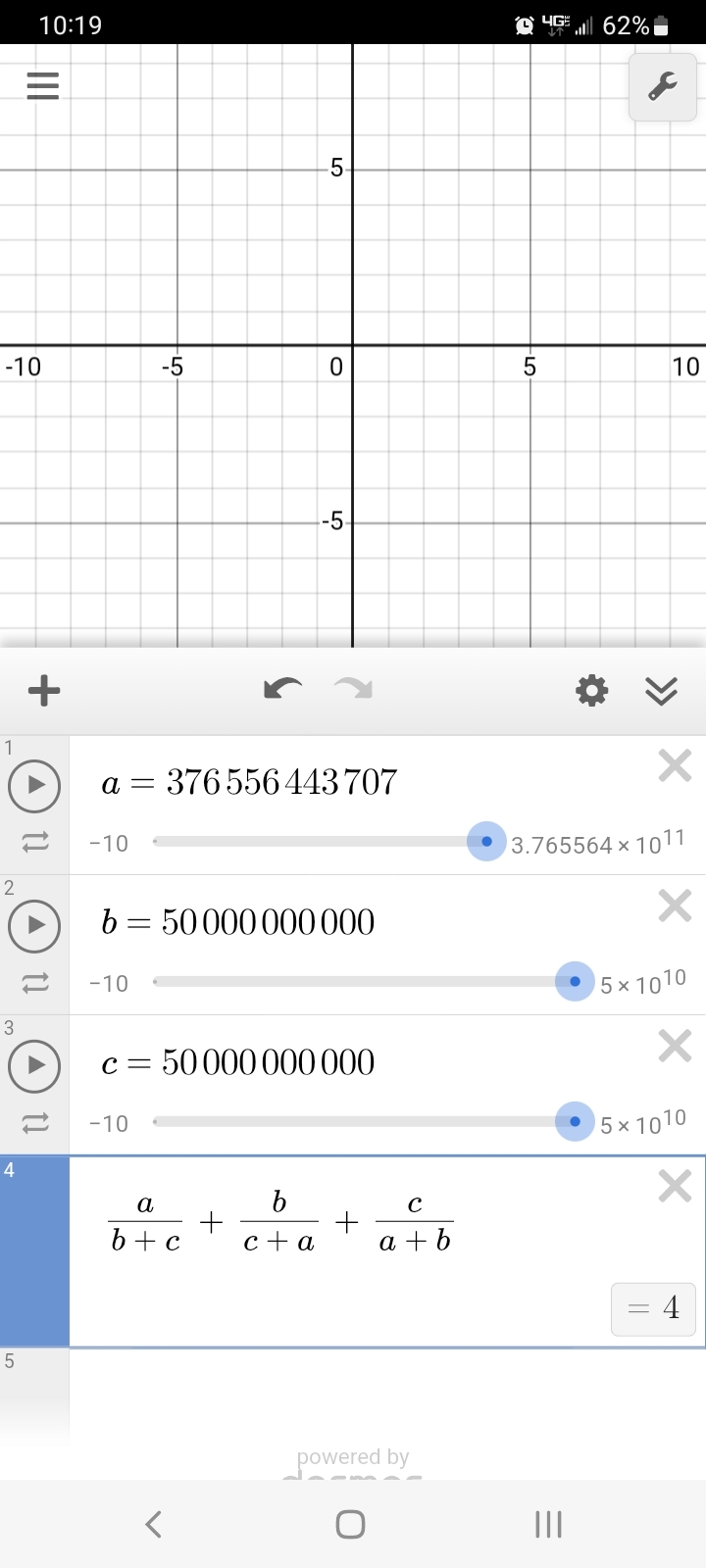
Now do it for a case where a,b, and c are pair wise not equal.
I have to admit, my solution is not correct anyways. I simple found a “solution” for which the margin of error is smaller than the calculator’s level of precision.
Sorry everyone, I cheated.
Is it the intersection of 3 curves?
Am I being trolled?
no, no I can’t
The solutions don’t quite fancy me as positive whole values, see for yourself.
An integer solution does exist.
Some discussion here
Not the same problem.
The original solution to this one was posted by +johncbaez999 on Google Plus and reposted here.
Ew please don’t link Reddit without warning.



